Describing Space

The length of the space diagonal of a cuboid with the length as $12 \mathrm{cm}$, breadth as $7 \mathrm{cm}$ and height as $5 \mathrm{cm}$, is

Find the length of the space diagonal of a cuboid with the length as $5 \mathrm{cm}$, breadth as $4 \mathrm{cm}$ and height as $3 \mathrm{cm}$.

A cuboid with the length as $5 \mathrm{cm}$, breadth as $4 \mathrm{cm}$ and height as $3 \mathrm{cm}$. The length of the face diagonal of the cuboid in the plane of breadth and height is $\sqrt{50} \mathrm{cm}$.

The number of face diagonals of a cuboid is 

Which of the following is not an example for Pythagorean quadruple ?

Find the angle between the diagonal of a cube and the diagonal of one of its faces. Where length of each side of a cube is $4$ unit.

Find the angle between the diagonal of a cube and the diagonal of one of its faces.

Which of the following is an example for Pythagorean quadruple ?

 Find the length of each diagonal of a rectangle of length $5$ units and width $3$ units?

Find the number of diagonals present in a cuboid?

Let $A\left(2, 1, -3\right)$ and $B\left(5, -8, 3\right)$ be two given points. Find the coordinates of the points of trisection of the line segment $AB$. 

In the figure below if the point $P$ is $\left(a,b,c\right)$, write the coordinates of the points $M,N,L,A,B$ and $C.$

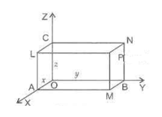
Write down the coordinates of point $A$ for the following cuboid:

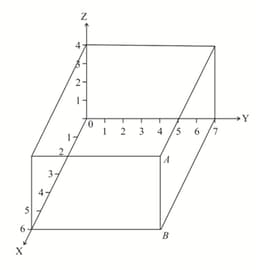
The theorem that we use in finding the length of space diagonal in rectangular prism is _____?

What is space in geometry?

Find the position vector of a point $R$ which divides the line joining two points $P$ and $Q$ whose position vectors are $P(\hat{i}+2\hat{j}-\hat{k})$ and $Q(-\hat{i}+\hat{j}+\hat{k})$ respectively, in the ratio $2 : 1$  internally

Given a line segment $AB$ joining the points $A(-4, 6)$ and $B(8, -3)$. Find the co-ordinates of the point of intersection.

Given a line segment $AB$ joining the points $A(-4,6)$ and $B(8,-3)$. Find the ratio in which $AB$ is divided by the y -axis.

Given $A=(-4, 3)$ and $B=(8,-6)$. In what ratio is the line joining $AB$ divides by the x-axis.

The line segment joining $A(2, 3)$ and $B(6, -5)$ is intercepted by its x-axis at the point $L$. Write the ordinates of the point $L$. Hence, find the ratio in which $L$ divides $AB$.